
Quiz Monkey
What do you want to know?
 |
Quiz Monkey |
| Science |
| Geometry |
| Angles |
| Trigonometrical functions |
| Polygons |
| Platonic solids |
| General |
Trigonometry is the branch of geometry that studies the relationships between the angles of triangles and the lengths of their sides.
If setting questions on this topic, you should probably prefix the question with "In trigonometry ... " (that'll get the contestants quaking in their boots) – and follow that up with " ... in a right-angled triangle ... " And just to be perfectly clear, the angle that were talking about (below) is one of the two angles that is not a right angle.
It's not actually as complicated as it sounds – honestly, it isn't – and as someone who did science 'A' levels, I think there's far too little science, and in particular too little maths, asked in quizzes. My partner (who did English and French) is always getting asked about novels that she studied for 'A' Level – and takes great delight in pointing it out, whenever it happens. I think it's high time the balance was adjusted.
And anyway ... this is 'O' Level!
| The length of the side opposite to an angle, divided by the length of the hypotenuse |
|
Sine (sin) |
| The length of the side adjacent to an angle, divided by the length of the hypotenuse |
|
Cosine (cos) |
| The length of the side opposite to an angle, divided by the length of the side adjacent to the same angle |
|
Tangent (tan) |
| The length of the adjacent side, divided by the length of the opposite side (the reciprocal of the tangent) |
|
Cotangent (cotan) |
| The reciprocal of the cosine (the hypotenuse divided by the opposite) |
|
Secant (sec) |
| The reciprocal of the sine (the hypotenuse divided by the adjacent) |
|
Cosecant (cosec) |
The thing to remember is that the Sine is equal to the Opposite divided by the Hypotenuse, the Cosine is the Adjacent divided by the Hypotenuse, and the Tangent is the Opposite divided by the Adjacent. Or, in algebraic notation:
| S = O/H | C = A/H | T = O/A |
There are various mnemonics that can help you to remember this. The one I was taught was:
| Some Officers Have | Curly Auburn Hair | Till Old Age |
Other versions listed in i before e (except after c), by Judy Parkinson (which I've referred to elsewhere on this website) are:
| Smiles Of Happiness | Come After Having | Tankards Of Ale |
| Some Old Hag | Caught A Hippie | Tripping On Acid |
| Some Old Horse | Caught Another Horse | Taking Oats Away |
Pick the one that suits you best!
A few other things that are worth knowing:
| The product of the tangent and the cotangent (of the same angle) is always equal to 1 (because the cotangent is the reciprocal of the tangent) |
| The ratio between the sine and the cosine (in other words, the result of dividing the sine by the cosine) is always equal to the tangent |
| It follows from Pythagoras's theorem that the square of the sine added to the square of the cosine is always equal to 1 |
| If the sum of two angles is 90 degrees, the sine of one is equal to the cosine of the other. |
Some important values:
| sin (0°), tan (0°), cos (90°) |
|
0 |
| cos (0°), tan (45°), sec (45°), sin (90°) |
|
1 |
| sin (30°), cos (60°) |
|
0.5 |
| sin (45°), cos (45°) |
|
1 / √2 |
| tan (90°) |
|
Not defined |
Apart from anything that's covered under General (below), there are four types of questions that you might get asked about polygons. Using a pentagon as an example, they are:
| • | What name is given to a polygon with five sides? |
| • | What is the exterior angle of a regular pentagon? |
| • | What is the interior angle of a regular pentagon? |
| • | What is the sum of the interior angles of a pentagon? |
The answers to these questions – and any similar ones that you're likely to get asked – are in the table below.
For the questions about the angles, however, rather than learning the answers individually, it's better if you can work them out. Before we can do this, we obviously need to know what we mean by an interior angle and an external angle.
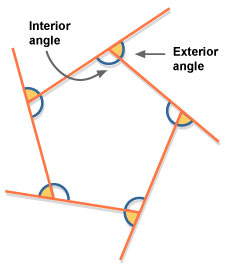
To show the interior and exterior angles, we need to extend one side of the polygon beyond the angle we're looking at – as in the diagram on the left (where each side is extended beyond one of the angles that it helps to form).
There are now two angles at each apex (point) of the polygon. The angle that's inside the polygon is known as the interior angle; the angle that's outside is known as the exterior angle.
Note that each pair of angles (one interior and one exterior) makes a straight line – in other words, the sum of each interior angle and its corresponding exterior angle is 180°.
The sum of the external angles, of any polygon, is 360°. To understand this, imagine an arrow drawn so that it points along one of the lines of the pentagon in the diagram. Now follow that line in the direction of the arrow, until you come to an angle. When you reach the angle, turn to move along the next line. Carry on until you get back to where you started; you'll then be pointing in the same direction as the one you started in – you'll have turned through 360 degrees.
Therefore, for a regular pentagon, each external angle must be 360° divided by 5, which is 72°.
The interior angle, therefore, is 180° – 72° = 108°.
To work out the interior angle for any regular polygon (one whose sides are all the same length and where all the angles are the same), the formula is:
a = 180 – (360/n)
where a is the angle in degrees and n is the number of sides.
Obviously, this only works for regular polygons. There's no way of calculating the internal angles of a polygon that isn't regular.
You can, however, work out the total value of all the internal angles – for any polygon, regular or irregular.
The sum of the exterior angles, of any polygon, is 360°. We know that the sum of each exterior angle and its equivalent interior angle is 180°; therefore, the sum of all the interior angles and all the exterior angles is 180 x n, where n is the number of sides. Therefore, the sum of all the interior angles is (180 x n) – 360, which is the same as saying (n – 2) x 180.
The following table gives the internal and external angles, and the sum of the internal angles, for any polygon that you're ever likely to be asked about in a quiz.
Note that the angles for the heptagon and the hendecagon are approximate. In practice, of course, you're unlikely to get asked about these, for the same reason, but I've included them for completeness – and because you're always likely to get asked about their names.
Similarly, I've included the values for 15– and 18–sided polygons, because they are whole numbers – although I've never heard their names asked about in a quiz, and in fact I don't even know if they have names!
A Platonic solid is a solid figure, all of whose faces, all of whose vertices and all of whose edges are congruent. There are five different Platonic solids:
| Number of vertices = (number of faces * number of vertices per face) / (number of faces that meet at each vertex) |
| Number of edges = (number of faces * number of sides per face) / (number of faces that share each edge, = 2) |
In practice, you're most unlikely to get asked any of the above except for the name of the solid figure with a given number of faces (as in the Name column). Or – perhaps more likely – you'll be given the name of the figure and asked how many faces it has.
Having said that ... I did once see a question on Eggheads about the number of edges on an icosahedron. But that was a multiple choice question. (The options, if I remember correctly, were 30, 40 or 50).
| Sum of the external angles of a polygon (doesn't have to be regular) |
|
360° | |
| Sum of the internal angles of a polygon with n sides (doesn't have to be regular) |
|
180 * n – 2 | |
| Surfaces of a cone |
|
2 (1 plane, 1 curved) | |
| Faces of a prism |
|
5 | |
| Minutes in a degree, seconds in a minute |
|
60 | |
| The angle between the hands of a clock, at one o'clock (or eleven o'clock) |
|
|
30° |
| Two arms meeting at a vertex |
|
Angle | |
| The highest point of an isosceles triangle (the point where the two equal sides meet); also of a pyramid or cone |
|
Apex | |
| A straight line that is approached, but not touched, by a given curve, as one of the variables in the equation of the curve approaches infinity |
|
Asymptote | |
| A straight line (strictly, a straight line segment) between two points on a curve |
|
Chord | |
| The locus of points in a plane that are equidistant from a certain fixed point; the conic section where the plane surface is normal (perpendicular) to the axis of the cone |
|
Circle | |
| Distance around the outside of a circle: equal to the diameter multiplied by pi (π) |
|
Circumference | |
| Two or more circles that have the same centre but different sizes |
|
Concentric | |
| Three–dimensional shape with only two surfaces: its volume is one third π r squared h, where h is the height |
|
Cone | |
| Two triangles whose corresponding sides and angles are equal (in layman's terms, the triangles are identical) |
|
Congruent | |
| Defined by the different intersections of a cone and a plane surface; circle, ellipse, parabola, hyperbola are the four types of |
|
Conic sections | |
| A three–dimensional figure with oblong (not necessarily square) faces |
|
Cuboid | |
| A line that bisects a circle |
|
Diameter | |
| The locus of points in a plane where the sum of the distances from any point on the curve to two fixed points is constant – conic section where the plane surface does not intersect with the base of the cone. A circle is a special case (where the two fixed points are the same) |
|
Ellipse | |
| The angle subtended by a side of a polygon and an extension of an adjacent side in a straight line (supplementary to the internal angle) |
|
External angle | |
| Plane and solid are the two branches of |
|
Geometry | |
| Isosceles triangle in which the distinct side and either of the two duplicated sides are in the golden ratio (its angles are 72°, 72° and 36°; the distinct side is the shortest) |
|
Golden triangle | |
| In a graph of the equation y = mx + c, m represents the |
|
Gradient of the line | |
| Three–dimensional figure like a spiral staircase or corkscrew; characteristic "double" form in DNA |
|
Helix | |
| Mathematical name for the Star of David |
|
Hexagram | |
| Conic section generated by the intersection of a right circular conic surface and a plane surface that cuts through both halves of the conic surface – i.e. the plane surface is not parallel to a generating straight line of the conic surface |
|
Hyperbola | |
| The longest side of a right–angled triangle – the one opposite the right angle |
|
Hypotenuse | |
| Triangle with two sides (and two angles) equal |
|
Isosceles | |
| Surface with only one side and one edge (boundary) – formed by twisting a strip of paper through 180° and joining the ends |
|
Möbius strip | |
| Perimeter of a regular polygon with n sides of length a |
|
n * a | |
| A triangle that does not contain a right angle |
|
Oblique | |
| The point on a graph where the axes meet – i.e. where all co–ordinates are equal to zero |
|
The origin (or pole) | |
| Conic section generated by the intersection of a right circular conic surface and a plane surface parallel to a generating straight line of the conic surface |
|
Parabola | |
| Ratio of the circumference and the diameter of a circle; also known as Archimedes' constant or the Ludolphine number (after early attempts to calculate it) |
|
Pi (π) | |
| The angle subtended at the centre of a circle by an arc of the circumference equal in length to the radius of the circle |
|
|
Radian |
| A line from the centre of a circle to the edge |
|
Radius | |
| A quadrilateral, all four of whose sides are the same length (of which a square is a special case; a diamond shape is another example) |
|
Rhombus | |
| A triangle where none of the sides or angles are equal |
|
Scalene | |
| Triangles with identical angles but sides of different lengths |
|
Similar | |
| "Four times pi r squared" is the formula for determining the surface area, and "four thirds pi r cubed" the volume, of a |
|
Sphere | |
| Everyday name for a reqular quadrilateral (one where all the sides and all the angles are equal); a rhombus where all four angles are right angles |
|
Square | |
| A straight line that touches a curve but doesn't cross it |
|
Tangent | |
| A solid figure with four triangular faces |
|
Tetrahedron | |
| Quadrilateral with one (and only one) pair of sides parallel (from the Greek for a table) |
|
|
Trapezium |
| "Half the base times the height" is the formula for determining the area of a |
|
Triangle | |
| The point where two lines meet to form an angle |
|
Vertex | |
© Haydn Thompson 2017–21